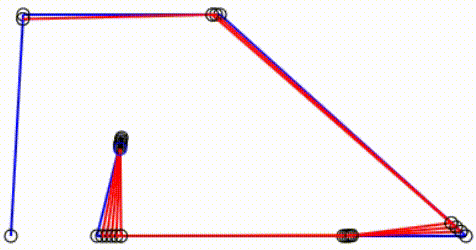
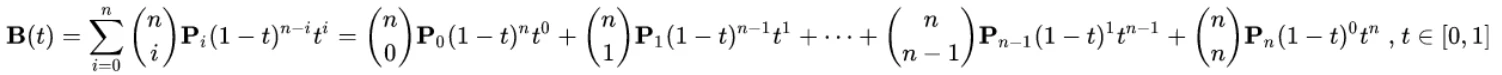前言
Canvas 提供的贝塞尔函数只能一次性绘制,而无法阶段性绘制,也就无法直接实现动画,并且只提供了二阶和三阶,有时候还需要更多阶。
最重要一点是,原生的贝塞尔曲线不太好做碰撞检测,判断一个点是否在一个封闭的直边多边形内部相对是比较容易的。
贝塞尔曲线于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由保尔·德·卡斯特里奥于1959年运用德卡斯特里奥算法开发,以稳定数值的方法求出贝塞尔曲线。贝塞尔曲线由 n 个控制点对应着 n-1 阶的贝塞尔曲线,并且可以通过递归的方式来绘制。
参考:
深入浅出贝塞尔曲线
贝塞尔曲线 javascript.info
从零开始学图形学:10分钟看懂贝塞尔曲线
用canvas绘制一个曲线动画——深入理解贝塞尔曲线
用Javascript+Canvas画N阶贝塞尔曲线
canvas实现高阶贝塞尔曲线
公式推导
下面是贝塞尔曲线的公式。
基本过程:
- 贝塞尔曲线由 n 个控制点绘制,各个点依次连成折线
- 第一个点到 n-1 个点都发出一个运动点,每个运动点以相同时间到达下一个相邻点。
- 一共有 n-1 个运动点,此时出现递归,可以视为 n-1 个控制点的贝塞尔曲线绘制。
- 注意,递归过程形成的所有运动点,都同时到达下一个相邻点。
- 最终,递归到一阶贝塞尔曲线,其运动点的轨迹就是要绘制的贝塞尔曲线。
这么说还是有些抽象,下面从一阶开始实际推导下。
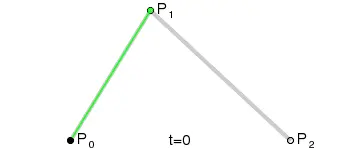
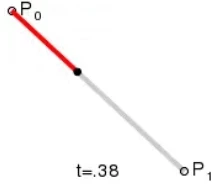
一阶
一阶贝塞尔曲线具有两个点,也就是一条直线。t 是单位时间,值为 [0, 1]。
很显然,运动点 Pt 坐标可以这么计算:Pt = P0 + (P1 - P0)t = (1 - t)P0 + tP1
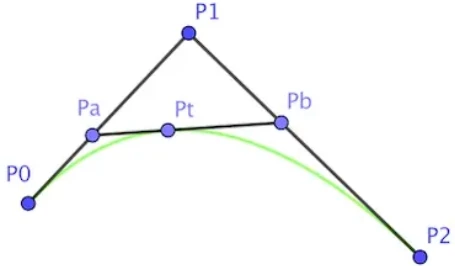
二阶
二阶贝塞尔曲线具有三个点,已经可以绘制为曲线。
Pa 和 Pb 两个运动点都要以相同时间到达下一个相邻点,于是有:|P0Pa| / |P0P1| = |P1Pb| / |P1P2| = t
每个运动点在各自线段上都可视为一阶贝塞尔曲线:Pa = (1 - t)P0 + tP1Pb = (1 - t)P1 + tP2Pt = (1 - t)Pa + tPb
将 Pa、Pb 代入 Pt,可以得到:Pt = (1 - n)^2P0 + 2t(1 - t)P1 + t^2P2
更多阶数也是如此,推导出的 Pt 已经符合公式了。
实现
明白了公式,就可以开始手写贝塞尔曲线了。
新建一个 Bezier 类,传入 canvas 上下文。
1 | class Bezier { |
计算运动点
也就是计算一阶贝塞尔曲线。
1 | // 计算两个点之间运动点位置 |
绘制曲线
设计上,采用增量更新,传入曲线点集合,只画最后两个点的连线。
1 | // 绘制贝塞尔曲线 |
递归降阶
这里递归将 n 阶贝塞尔曲线降为 1 阶,每次递归都调用 calcMotionPoint() 计算当前运动点(下一阶的控制点)位置,最后 1 阶的运动点就是曲线上的点,将其加入曲线点集合数组,并调用 drawCurve() 增量绘制。
绘制出控制点之间的连线,更加直观。
1 | // 计算和连线各个控制点和运动点 |
静态绘制
1 | draw(controlPoints, t = 1) { |
动画绘制
1 | // 绘制动画 |
完整代码
1 | class Bezier { |
使用
1 | const points = [ |